이진 탐색 트리(Binary Search Tree)
- 각 노드의 왼쪽 subtree의 key 값은 노드의 key 값보다 작거나 같아야 하고
- 각 노드의 오른쪽 subtree의 key 값은 노드의 key 값보다 커야 한다.
- 모든 노드에서 만족해야 함.
search 연산에서 장점이 있음 O(h) -> 높이를 적정하게 유지하는 것이 중요.
class BST:
def __init__(self):
self.root = None
self.size = 0
def __len__(self):
return self.size
def __iterator__(self):
return self.root.__iter__()
# yield
def find_loc(self, key): # key 값 노드가 있다면 해당 노드 return 없다면 노드가 삽입될 부모노드 리턴
if self.size == 0 :
return None
p = None
v = self.root
while v != None:
if v.key == key : return v
elif v.key < key :
p = v
v = v.right
else:
p = v
v = v.left
# key가 T에 없는 경우
return p
def search(self, key):
v = self.find_loc(key)
if v == None:
return None
else:
return v
def insert(self, key):
p = self.find_loc(key) # O(h)
if p == None or p.key != key:
v = Node(key)
if p == None: # 현재 노드가 루트가 됨
self.root = v
else: # p != None and p.key != key -> 새로운 키가 들어왔다는 뜻
v.parent = p
if p.key >= key:
p.left = v
else:
p.right = v
self.size += 1
return v
else:
print("key is already in trees")
return None
# update links삭제 연산(delete) : deleteByMerging, deleteByCopying
노드 x를 찾고 deleteByMerging에서 삭제하면 됨

여기서 x의 왼쪽 서브 트리를 L, 오른쪽 서브트리를 R이라 했을 때
L에서 가장 큰 노드에 R을 붙여야 함
x의 부모 노드는 L의 부모 노드로 업데이트
특별한 경우
1. a == None 인 경우 ( L이 None일 때)
- R을 그냥 붙이면 됨
2. x == root 인 경우 (삭제하려는 노드가 root일 때)
- BST의 root 노드를 변경해줘야 함
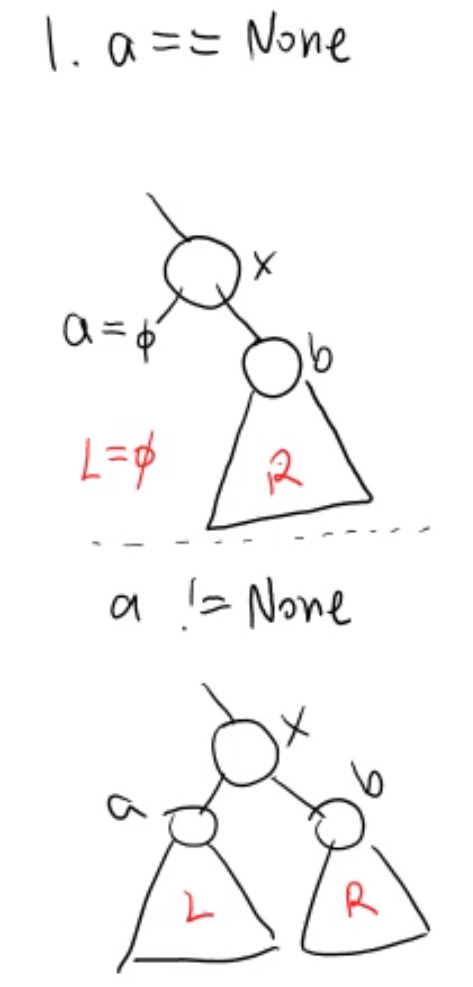
deleteByMerging - deleteByCopying 둘 다 O(h) -> m을 찾는 과정에서 가장 많은 시간 소요
def deleteByMerging(self, x):
a, b = x.left, x.right
pt = x.parent
# c => x 자리를 대체할 노드
# m => L 에서 가장 큰 노드
if a! = None:
c = a
m = a
while m.right:
m = m.right
if b != None:
b.parent = m
m.right = b
else: # a == None
# x 자리를 대체하는 c가 b가 됨
c = b
# pt가 None인 경우 아닌 경우 나눠서 생각 (pt가 None이라는 것은 x가 root)
if pt == None:
# root = x라는 뜻
self.root = c
if c:
c.parent = None
else:
if c:
c.parent = pt
if pt.key < c.key:
pt.right = c
else:
pt.left = c
self.size -= 1def deleteByCopying(self, x):
# 1. pt의 link 수정
# 2. x의 pt link 수정
참고 - https://www.youtube.com/watch?v=Bhprzw_1kb0&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=26
https://www.youtube.com/watch?v=VVhmgQIJCu8&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=27
'Computer Science > Data Structure' 카테고리의 다른 글
| Python 힙 구현 (0) | 2022.04.23 |
|---|---|
| 자료구조, 자료형, 추상 자료형 (0) | 2022.03.25 |
| 이진트리 - 정의와 순회 (0) | 2022.01.01 |
| 힙 자료구조 - insert 연산 (0) | 2022.01.01 |
| 힙 자료구조 - make heap 연산 (0) | 2022.01.01 |


댓글