
https://programmers.co.kr/learn/courses/30/lessons/12905
코딩테스트 연습 - 가장 큰 정사각형 찾기
[[0,1,1,1],[1,1,1,1],[1,1,1,1],[0,0,1,0]] 9
programmers.co.kr
전형적인 DP 문제다. DP를 만족하기 위해서
1. 최적 부분 구조 (Optimal Substructure)
- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
2. 중복되는 부분 문제 (Overlapping Subproblem)
- 동일한 작은 문제를 반복적으로 해결해야 한다.
이 정사각형 문제도 위의 두 조건을 만족한다.
처음엔 완전 탐색으로 풀었는데, 효율성 테스트에서 시간 초과가 나서 생각해보니 dp로 풀어야겠다는 생각을 했다.
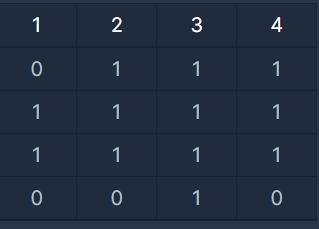
행과 열 (0 , 0)로 시작한다고 했을 때 (1 , 1) 위치에서 최대 정사각형 크기가 2가 되려면
(0 , 0), (1 , 0), (0 , 1) 들이 모두 1이어야 한다. 여기선 (0, 0) 이 0 이기 때문에 최대 정사각형 크기는 1이 된다.
(i , j)에서 최대 정사각형 크기는 즉, dp[i][j]는
dp[i][j] = min( dp[i -1][j - 1], dp[i, j -1] , dp[i - 1, j] ) +1과 같다.
나의 풀이
def solution(board):
dp = [[0]*len(board[0]) for _ in range(len(board))]
answer = 0
for i in range(len(board)):
for j in range(len(board[0])):
dp[i][j] = board[i][j]
if i-1 >=0 and j-1 >=0 and dp[i][j] !=0:
dp[i][j] = min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1]) + 1
answer = max(answer,dp[i][j])
return answer**2'Programming > Programmers' 카테고리의 다른 글
| [프로그래머스] 파일명 정렬 (Python) (0) | 2021.11.07 |
|---|---|
| [프로그래머스] 압축 (Python) (0) | 2021.11.06 |
| [프로그래머스] 방금 그곡 (Python) (0) | 2021.11.04 |
| [프로그래머스] 방문 길이 (Python) (0) | 2021.11.04 |
| [프로그래머스] 쿼드 압축 후 개수 세기 (Python) (0) | 2021.11.04 |




댓글