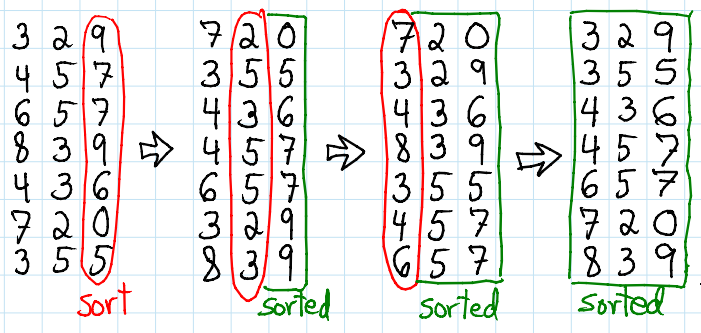
기수 정렬은 각각의 자릿수를 기반으로 정렬해나가는 알고리즘이다.
안정 정렬에 속하고, 비교 정렬을 수행하지 않아서 조건이 맞는 상황에서 빠른 정렬 속도를 보장하는 알고리즘이다.
- 장점 : 문자열, 정수 정렬 가능 , 일부에서 nlogn 보다 빠르게 동작(비교 연산을 하지 않음)
- 단점 :
- 자릿수가 없는 것은 정렬할 수 없음. (부동 소숫점)
- 중간 결과를 저장할 bucket 공간이 필요함.
기수 정렬의 방법으로는 LSD와 MSD 두 방법이 있는데
MSD (Most-Significant-Digit)과 LSD (Least-Significant-Digit)을 비교
MSD는 가장 큰 자릿수부터 Counting sort 하는 것을 의미하고, LSD는 가장 낮은 자리수부터 Counting sort 하는 것을 의미함. (즉, 둘 다 할 수 있음)
- LSD의 경우 1600000과 1을 비교할 때, Digit의 개수만큼 따져야 하는 단점이 있음. 그에 반해 MSD는 마지막 자릿수까지 확인해 볼 필요가 없음.
- LSD는 중간에 정렬 결과를 알 수 없음. (예) 10004와 70002의 비교) 반면, MSD는 중간에 중요한 숫자를 알 수 있음. 따라서 시간을 줄일 수 있음. 그러나, 정렬이 되었는지 확인하는 과정이 필요하고, 이 때문에 메모리를 더 사용
- LSD는 알고리즘이 일관됨 (Branch Free algorithm) 그러나 MSD는 일관되지 못함. --> 따라서 Radix sort는 주로 LSD를 언급함.
- LSD는 자릿수가 정해진 경우 좀 더 빠를 수 있음.
MSD 같은 경우는 해당 자릿수까지 정렬이 완료되었는지 데이터를 검사해야 하므로 성능이 반감될 수 있다.
def counting_sort(arr,digit):
n = len(arr)
# 변경된 정렬 값을 유지할 output 리스트
output = [0] * n
# 0 ~ 9 까지의 자리수 수를 더할 counting
counting = [0] * 10
# 각 배열의 원소의 자리수에 대한 개수를 counting 리스트에 추가
for i in range(n):
index = int(arr[i]/digit)
counting[index % 10] += 1
# 이전 count 값을 차례로 더해주게 되면, 해당 위치까지 몇개의 원소가 있는지 확인 가능
for i in range(1,10):
counting[i] += counting[i-1]
# 안정 정렬이므로 리스트 뒷부분 부터 차레로 위치 변경해준다.
i = n - 1
while i>=0 :
index = int(arr[i]/digit)
# ouput에서 -1 해주는 이유는 counting의 값은 실제 인덱스 값보다 하나 큼
# ex) n = 10 이라면 counting[9] <- 가장 끝 원소 == 10 실제로 output끝 값은 output[9]
# 이 부분은 실제로 코드를 한줄씩 디버깅 하거나 직접 적으면서 생각해야 이해 됨
output[counting[index % 10] - 1] = arr[i]
counting[index % 10] -= 1
i -= 1
# 정렬된 리스트를 실제 리스트와 값 변경
for i in range(n):
arr[i] = output[i]
def radix_sort(arr):
# 배열의 최대 값을 기준으로 자리수 비교
maxValue = max(arr)
# 일의 자리부터
digit = 1
while int(maxValue/digit) > 0 :
#counting sort
counting_sort(arr,digit)
digit *= 10수행시간 비교
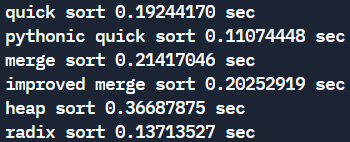
참고 -
'Computer Science > Algorithm' 카테고리의 다른 글
| #08 파이썬 내장 정렬(Tim Sort) (0) | 2022.01.08 |
|---|---|
| #08 계수 정렬(Counting Sort) (0) | 2022.01.07 |
| #06 힙 정렬(Heap Sort) (0) | 2022.01.07 |
| #05 병합 정렬(Merge Sort) (0) | 2022.01.06 |
| #04 퀵 정렬(Quick Sort) (0) | 2022.01.06 |




댓글